» 佐賀の県立高校入試問題　よく分かるワンポイント数学「面積比」

 

『Ａの面積は、Ｂの面積の何倍か。』

 

という問題がよくある。

 

Ａは三角形で、Ｂは平行四辺形であったり。

 

ＡもＢも両方とも三角形であったり。

 

 

いずれにしても、このように『面積が何倍か』という問いが出たら、比を求めれば良いと思ってちょーだい。

 

『Ａの面積とＢの面積の比は、何対何か。』

 

ということ。

 

 

Ａ：Ｂの面積比を出す。

 

で、それが a：b だったとする。

 

そしたら、a÷b で答えが出る。

 

 

例えば、こういうことね。

 

三角形ＯＤＥの面積は、平行四辺形ＡＢＣDの面積の何倍か。

↓

三角形ＯＤＥ：平行四辺形ＡＢＣD　の面積比を出す。

↓

３：２８　になった。

↓

３÷２８　をする。

↓

（答え）２８分の３ 倍

 

この流れね。

 

 

でもって、面積比といえば「三角形の面積比」が全て。

 

すべての多角形は三角形を組み合わせたものだからね。

 

だから面積比といえば「三角形の面積比」。

 

そして、三角形の面積比といえば、これ。

 



 

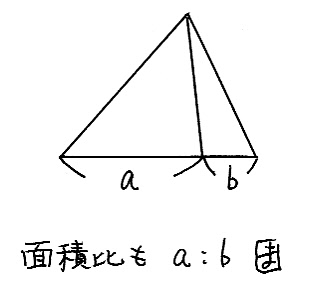
底辺の比がそのまま面積比と等しくなるってやつ。

 

底辺の比といえば、結局「線分の比」だよね。

 

線分の比といえば、これ。

 



 

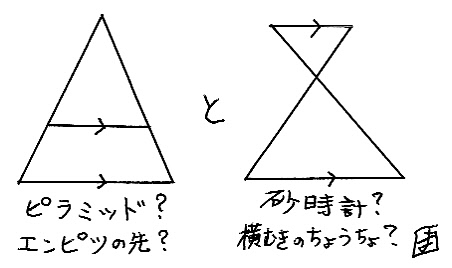
全てはここからだ。

 

難しそうに見える問題も全てこれの組み合わせ、と思ってちょーだい。