計算の工夫に感動できるか
色がよく見えないな・・・。
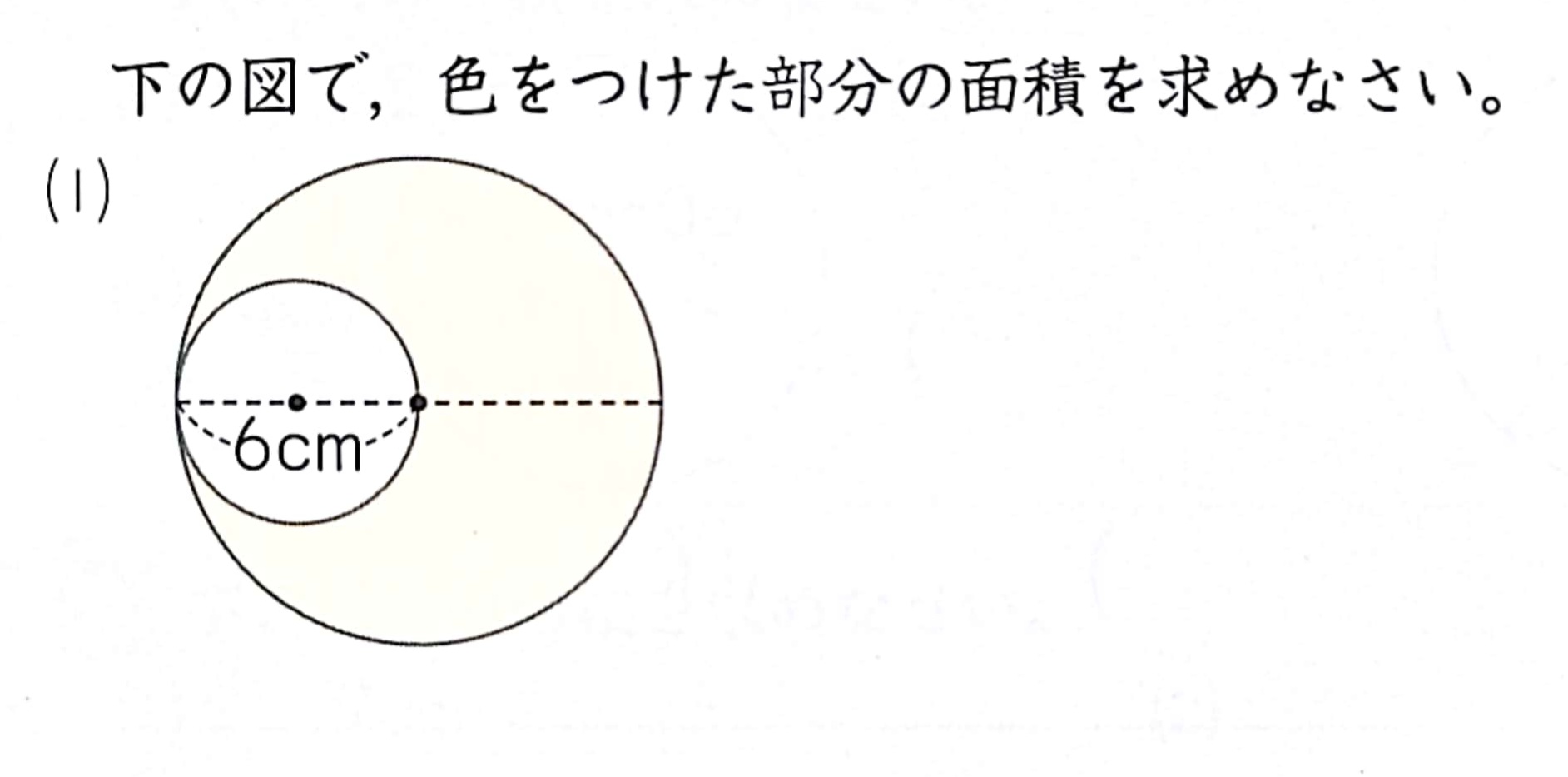
要するに大きい円から中の小さい円を引いた残りの面積が答えになる問題。
6年生でやるじゃん。
求める式はこうなる。
6×6×3.14-3×3×3.14
これをそのまま計算の順序通りにやると
6×6×3.14-3×3×3.14
=36×3.14-9×3.14
=113.04-28.26
=84.78
で、84.78㎠ が答え。
これ、順序を工夫して計算するとこんなことが出来る。
6×6×3.14-3×3×3.14
=36×3.14-9×3.14
=(36-9)×3.14
=27×3.14
=84.78
ってね。
要するに3.14との掛け算が1回で済むから楽でしょってことだ。
これは昨日書いた「共通点」を見出すことで計算の工夫が出来て勉強が楽しめるってことに通じる事柄だ。
問題集の模範解答では、この工夫する解き方が当たり前のように書かれてあるのよね。
でも、オレは最初っからその工夫を教えることはしない。
むしろ順序通りの計算をやってもらう。
まず、円周率との掛け算を2回やるくらいの計算はさっさと簡単にこなす計算力を身につけてほしい。
でもって、その元々の計算をやってないと工夫することで楽になるという感動を感じることは出来ないと思ってるからだ。
「おー、こうすりゃ簡単になるじゃん」
面倒くさいことを知ってないと簡単便利の素晴らしさが薄れる。
感動してほしいなーって思うよ。
しかしそれよりも何よりも、まずは普通にやって間違わない計算力を大事にしたいんだよね。
☆こちらもどうぞ

このページに対してのコメント