» 変化の割合

 

関数のお話。

 

数日前にインスタでショート動画をアップした。

 

それをブログでも念押ししておきたい。

 

関数における「変化の割合」についてだ。

 

 

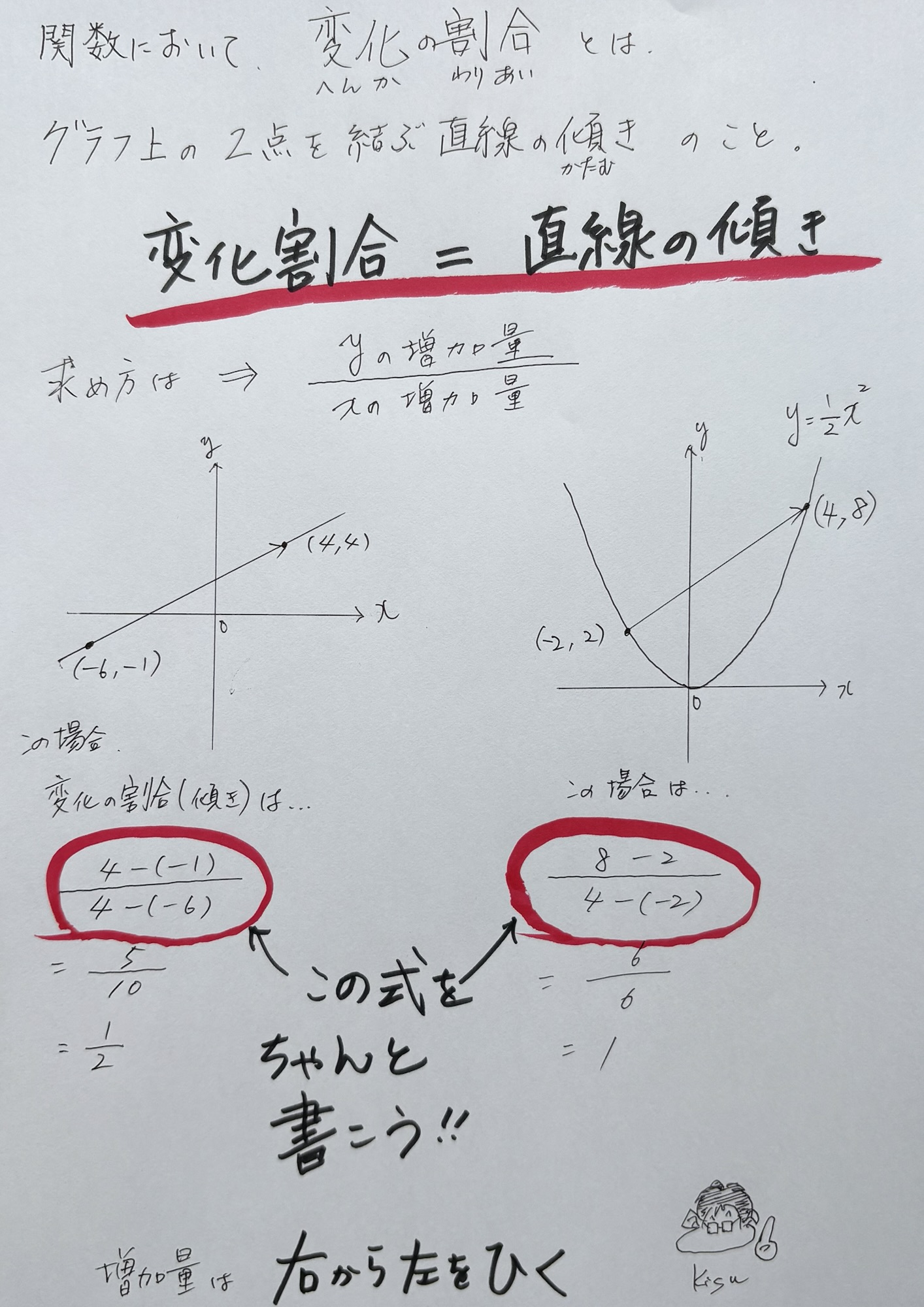
変化の割合というのは、ｙの増加量がＸの増加量の何倍かを表した数で、直線の傾きと等しい。

 

中２の１次関数、そして中３の２乗に比例する関数で勉強している。

 

まず中２で最初に学び、中３でも全く同じことをしている。

 

１次関数の式を求める時にまずこれを求める計算を覚えてもらう。

 

 

この時、増加量を求める計算は（右から左を引く）と覚えてもらう。

 

正の数だろうが負の数だろうが、どっちの数が大きかろうが小さかろうが、常に右から左を引いてもらう。

 

 

これ、反対に左から右を引いても同じ答えになるから不徹底な人もいるんだけど、オレはこだわってる。

 

常に同じ計算をする。

 

これがミスを防ぐための鉄則だ。

 

 

そして最初の式は書く。

 

下の画像を参考にしてほしい。

 

この最初の引き算分数式をこのように書くことでミスは激減する。

 

 

変化の割合を求めるという計算は本格的な関数の入り口で、最初の重要ポイントね。

 

ここはとにかく全員に徹底して欲しい内容だよ。

 

 

↓ショート動画を続々更新中☆

⇒『ホクトInstagram』

 

⇒『入塾をお考えの方へ』