» 円周率のかけ算で学べること

 

「円の面積の求め方は？」

 

「半径 × 半径 × ３.１４」

 

「よく言えましたー。じゃあ、計算してみましょー。」

 

「げー。」

 

他愛もない小芝居から入ってみたが、自分が小学校の時、算数で円周率のかけ算するのがとってもイヤだったなーという記憶がある。

 

 

例えばこんな問題があるでしょ。

 



 

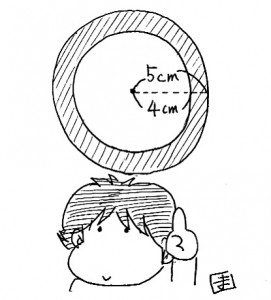
雑な図でゴメンナサイね。

 

斜線部分の面積を求めなさいという問題。

 

そのまんまやればこういう計算になるね。

 

５ × ５ × ３.１４ = ７８.５

４ × ４ × ３.１４ ＝ ５０.２４

７８.５ － ５０.２４ ＝ ２８.２６

 

で、答えが ２８.２６㎠ となる。

 

 

でもこれって、ちょっと計算を工夫すればこうなるよね。

 

５ × ５ × ３.１４ － ４ × ４ × ３.１４

＝ ２５ × ３.１４ － １６ × ３.１４

＝（２５ － １６） × ３.１４

＝ ９ × ３.１４

＝ ２８.２６

 

答え ２８.２６㎠

 

こうすれば、３.１４をかける計算が１度で済んでしまうわねー。

 

でもね、これを「楽だねー」とか「スゴいねー」とは、最初のそんまんまの順番での計算をやった経験がないと実感出来ない場合が多いと思うよ。

 

だから、うちの授業では特に何も言わずに自分の思うようにやってもらう。

 

そうすると、ほとんどの子が最初のやり方で計算していくよ。

 

それを苦も無く計算して正解出来るならそれで構わないし。（むしろそのくらいの計算力が欲しい）

 

そこで計算に苦しむようなら、それこそそのまんまの順番で求めていくことを要求する。

 

カッコでくくるのは、そのまんまの順番での計算を十分に経験した上でやってもらった方がイイと思ってる。

 

 

もちろん、その時の到達度によってカッコでくくるという計算をどんどんやってもらう場合もあるさ。

 

でも、最初の経験が十分ではないのなら、塾ではそこだけのトレーニングで終わっても構わない。

 

カッコでくくる計算は小学校の授業でやることもあるだろうし、中学校に入れば必ずやるからそこで経験すればイイじゃないか。

 

 

そういう点でも、１人１人をよく見てないといけないね。

 

その上で、この子には今ここで何を学んでもらいたいかをシッカリこっちが持ってた方がイイなーと思う。

 

以上、小学生算数教室のつぶやき。