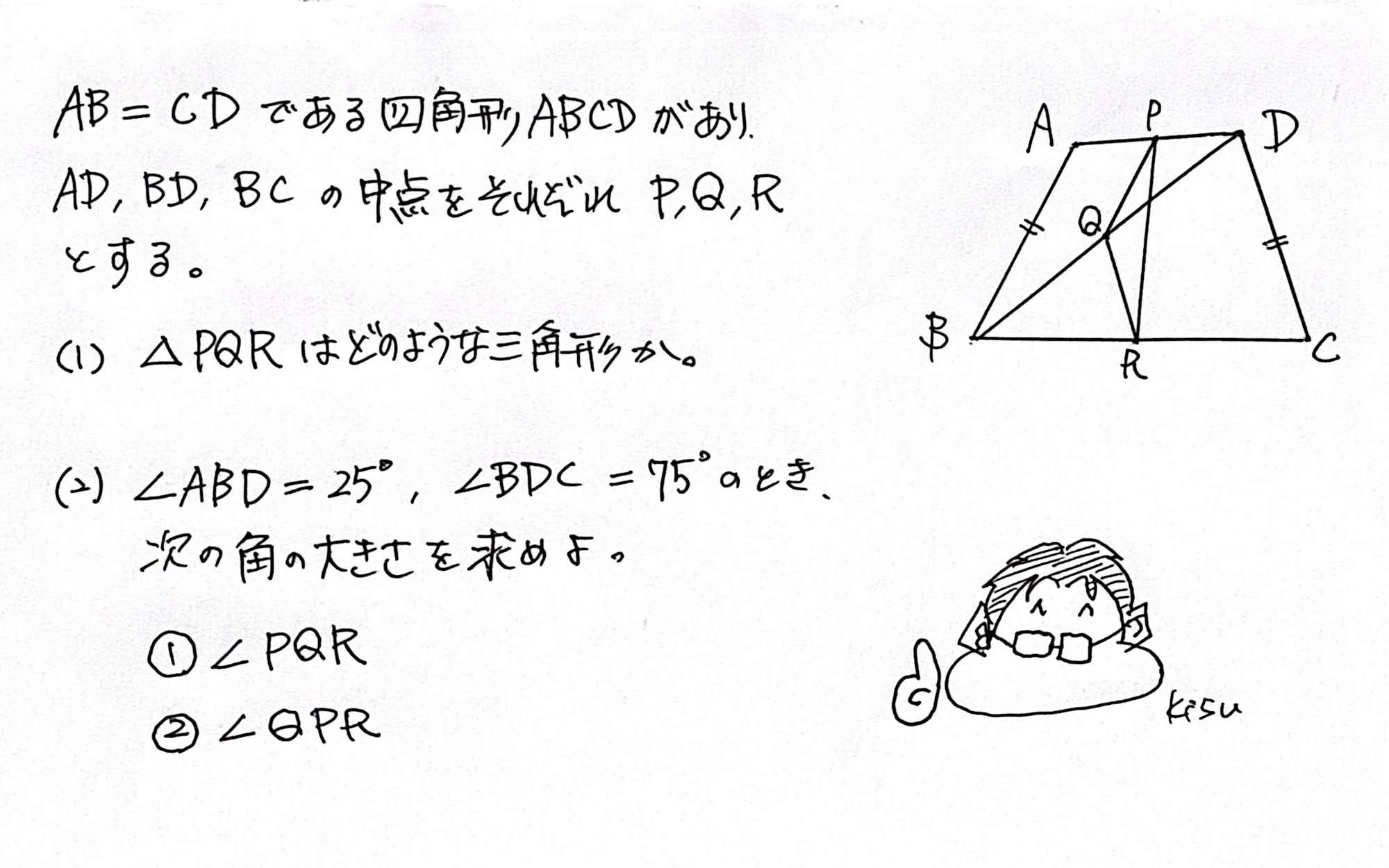
» 気づくための手順

 

 

上の問題を考えてみよう。

 

中３の数学だ。

 

(1)は、ほとんどの人が見た目で二等辺三角形と答えるだろう。

 

何故かが説明できなくても二等辺三角形に見えるから。

 

そうやって解答用紙を埋めるのも大事。

 

しかし、(2)の問題は理屈が分かってないと気づけないのよ。

 

 

さて、どうやったら気づけるか。

 

天才的なひらめきなどは必要無い。

 

学んだことを引き出すだけ。

 

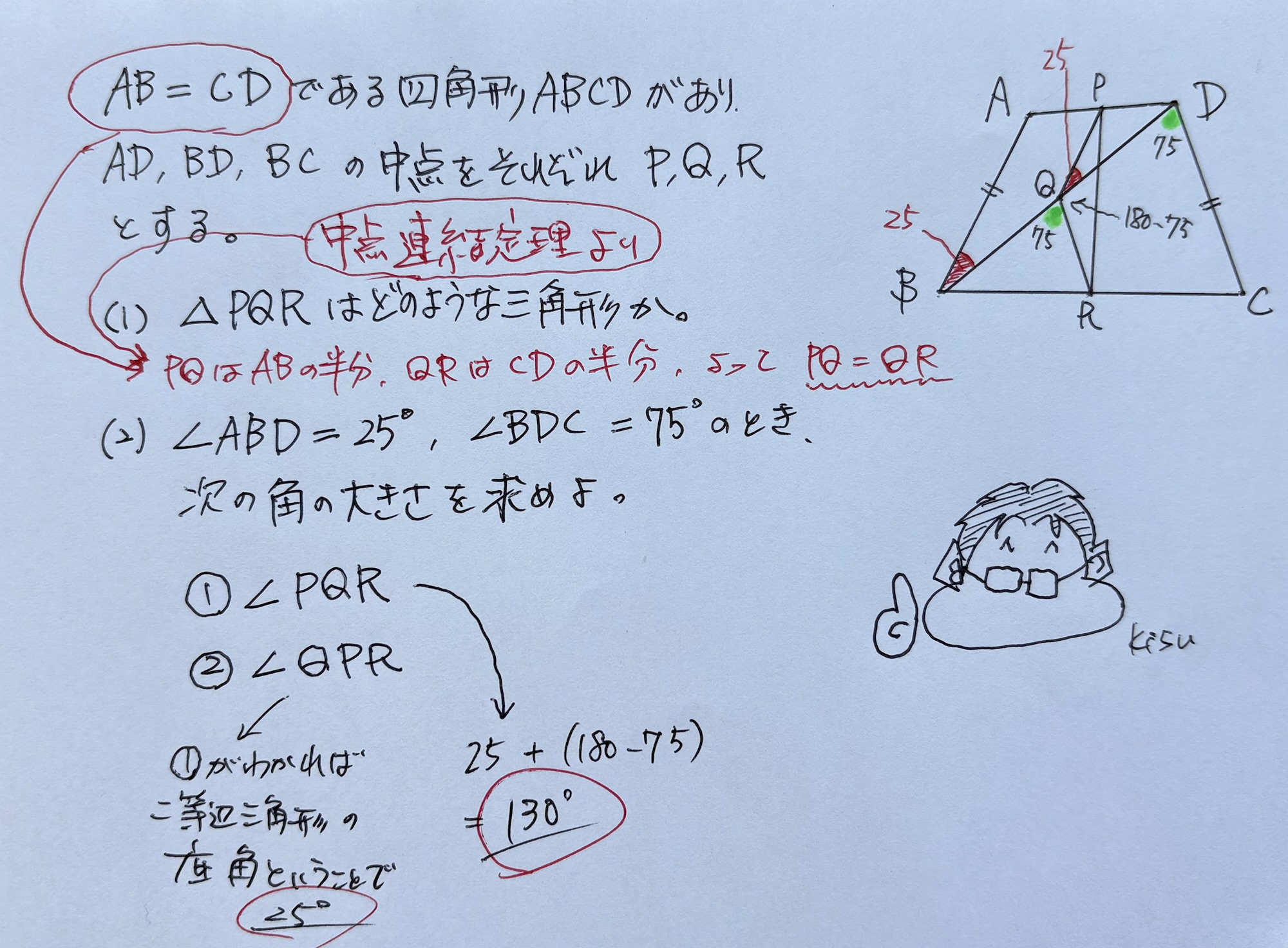
三角形の２辺の中点と中点を結んだ線分は、その下の底辺と平行になり長さは半分になる。

 

この中点連結定理を学んだ後に解く問題だから、ABとPQは平行、CDとQRも平行になる。

 

そこで、「平行」といえば中２で学んだ平行と角度を思い出す。

 

２直線が平行なら同位角と錯角が等しくなる。

 

そこから、与えられた条件と照らし合わせる。

 

∠ABD、∠BDC、２つの角度が分かってる。

 

その２つと同位角または錯角になる角度は無いか、注目するのは問われている∠PQRの部分・・・。

 

ここまでくれば高い確率で解き方に気づく。

 

 

「気づく」方法、それは学んだことを思い出す作業なのだ。

 

発想とは応用力などというものではない。

 

思い出す作業。

 

そのことを常に意識して問題を解くようにすれば、少しずつ問題の見え方が変わってくるよ。

 

 

↓ショート動画を続々更新中☆

⇒『ホクトInstagram』

 

⇒『入塾をお考えの方へ』