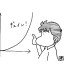
変化の割合①
Yの増加量÷Xの増加量
で求めた値を「変化の割合」という。
一次関数でいうところの「直線の傾き」にあたる。
変化の割合が大きいほど、直線の傾斜が大きいってことになる。
例えばこれを受験勉強に当てはめてみよう。
Xの増加量を日数の経過、Yの増加量を成績の伸び、とでもおいてみようか。
この場合の変化の割合は、一定日数における成績の伸びってことになる。
入試本番までに目標のレベルまで成績を伸ばすためには、この変化の割合を大きくしていくべきだろう。
そのためにはどうすればよいか。
これをまず自分で意識しないと始まらない。
っていうか、そうしないとこの変化の割合は絶対に大きくならない。
昨日までにやった9月度志望校判定テストの結果も、それらを意識するための大切な材料になるよ。
そうしなければね。
この話、なんとなく明日まで続けちゃおう。

☆こっちも毎日更新中↓
「塾長の裏ブログ」もどうぞ。

このページに対してのコメント